LaTeX v kostce - matematika

J) Matematika

Matematický režim se nastaví vstupem do jednoho z dále uvedených prostředí. V těchto prostředích nesmí být žádný prázdný řádek. V matematickém režimu se používají fonty nezávislé na nastaveních vně matematického prostředí s výjimkou nastavení velikosti - to platí i po vstupu do matematického režimu.

Matematická prostředí:

\begin{math} \end{math} (ekvivalentně $ $ nebo $ $) ... vzorec v textu
\begin{displaymath} \end{displaymath} (ekvivalentně \[ \] ) ... vzorec mimo text bez čísla
$$ $$ ... TeXovské "prostředí" pro vzorec mimo text
\begin{equation} \end{equation} ... číslovaná rovnice (vzorec)
\begin{eqnarray} \end{eqnarray} ... zarovnané číslované rovnice (vzorce} podle zarážek
\begin{eqnarray*} \end{eqnarray*} ... zarovnané nečíslované rovnice (vzorce) podle zarážek

Některá prostředí zařizují automatické číslování rovnic. Číslo je odvozeno od pořadí rovnice a od čísla oddílu, ve kterém se nachází. Uživatel může standartně číslování ovlivnit jen způsobem "tuto rovnici čísluj - nebo nečísluj" s jednou výjimkou - v TeXovském prostředí $$ $$ funguje TeXovský příkaz \eqno - a to tak, že na okraj stránky přidá řetězec, který následuje za \eqno (např. $$x^2+3=4 \eqno(2) $$).

Pozn. TeXovské prostředí $$ $$ nezvyšuje hodnotu čítače rovnic equation. Pokud tuto hodnotu chceme zvýšit o jedničku i v tomto případě, pak (nejlépe dovnitř $$ $$) umístíme příkaz \refstepcounter{equation}.

Příklad1:

    \begin{eqnarray}
    x &= & 8(x-9) + y + 14 \nonumber \\
    x &= & 8(x-9) - y + 15 \\
    -3x &= & 0.5x + 0.1 y - 103  
    % příkaz \\ za posledním řádkem by LaTeX pochopil
    % jako že má následovat ještě jedna rovnice a 
    % očísloval by prázdný řádek
    \end{eqnarray}

Pokud se hned za rovnici přidá klíčové slovo \nonumber, nebude tato číslovaná. Velikost mezery mezi řádky v tomto prostředí je určena délkovým registrem \jot. Pozn.: vytváření sloupců v prostředí eqnarray funguje asi následujícím způsobem:

prohlédnou se všechny řádky v eqnarray a rozhodne se o počtu sloupců podle řádku s největším počtem tabulátorů &
pokud je na některém řádku méně než tento největší počet tabulátorů, jakoby se doplní na konec tohoto řádku příslušný počet tabulátorů (před případné \\ a \nonumber)
šířka daného sloupce se nastaví podle položky, která je ze všech řádků nejširší, přičemž se nikdy nejde pod jistou minimální šířku

Pokud v prostředí eqnarray místo & text (kde text je nějaký text - kus vzorce) napíšeme \lefteqn{text}, pak se to chová jako & text až na to, že se šířka textu při nastavování zarážek chápe jako nulová a text se zarovnává podle levé zarážky. To se dá využívá pro složitější rozdělování rovnic na více řádků: např.:

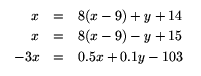
Příklad2:

	     
    \begin{eqnarray*}
    \lefteqn{y=a+b+c+d+e+f+g-} \\
    & & -\sqrt{a+b+c+d+e+f+g}
    \end{eqnarray*}

Matematickou obdobou (se všemi detaily) textového prostředí tabular je prostředí array (musí být vnořeno v prostředí displaymath nebo equation - v případě, kdy chceme, aby matice byla mimo text, a nebo mezi $ $ - pokud chceme, aby matice byla v textu).

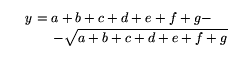
Příklad3:

    \begin{equation}
    \begin{array}{ccc@{\quad}r}
    x & x-y+z & z & 31.27 \\
    x-y & y+z & -z & 2.32 \\
    x & y & 2 z & -4,36 \\
    \end{array}
    \end{equation}

Příklad4:

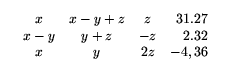
    $$\left( \begin{array}{ccc@{\ }r}
    a & b & c & -10.15 \\
    a & b & c & 3.1 \\
    a & 0.3 b & 0.1c & -24 \\
    \end{array} \right)$$

Příklad5:

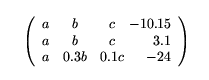
    $$f(x) = \left\{ \begin{array}{r@{\quad}c}
    y, & x > \pi \\
    -y, & x \leq \pi \\ \end{array} \right.
    $$

Nastavení písma v matematice:

Číslo rovnice je ve třídě article jednoduché arabské číslo uzavřené v kulatých závorkách. Ve třídách book a report je místo jednoho čísla dvojčíslí ze dvou arabských číslic oddělených tečkou, kde první položka je číslo kapitoly a druhá je pořadí rovnice v dané kapitole (např. (2.3)).

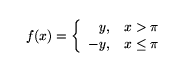
Matematické symboly:

Šipky:

`\leftarrow`	`\Leftarrow`	`\longleftarrow`	`\Longleftarrow`
`\leftrightarrow`	`\Leftrightarrow`	`\longleftrightarrow`	`\Longleftrightarrow`
`\hookleftarrow`	`\leftharpoonup`	`\leftharpoondown`	`\rightleftharpoons`
`\uparrow`	`\Uparrow`	`\downarrow`	`\Downarrow`
`\updownarrow`	`\Updownarrow`	`\nearrow`	`\searrow`
`\swarrow`	`\nwarrow`	`\mapsto`	`\longmapsto`
`\leadsto`

a ještě slova, kde je right místo left (kromě těch, kde je left i right)

Relace:

`\leq`	`\geq`	`\prec`	`\succ`
`\preceq`	`\succeq`	`\ll`	`\gg`
`\subset`	`\supset`	`\subseteq`	`\supseteq`
`\sqsubset`	`\sqsupset`	`\sqsubseteq`	`\sqsupseteq`
`\in`	`\ni`	`\vdash`	`\dashv`
`\equiv`	`\sim`	`\simeq`	`\asymp`
`\approx`	`\cong`	`\neq`	`\doteq`
`\propto`	`\models`	`\perp`	`\mid`
`\parallel`	`\bowtie`	`\Join`	`\smile`
`\frown`

pozn: pro \Join je potřeba standartní balík latexsym

Binární operátory:

`\pm`	`\mp`	`\times`	`\div`	`\ast`
`\star`	`\circ`	`\bullet`	`\cdot`	`\cap`
`\cup`	`\uplus`	`\sqcap`	`\sqcup`	`\vee`
`\wedge`	`\setminus`	`\wr`	`\diamond`	`\bigtriangleup`
`\bigtriangledown`	`\triangleleft`	`\triangleright`	`\lhd`	`\rhd`
`\unlhd`	`\unrhd`	`\oplus`	`\ominus`	`\otimes`
`\oslash`	`\odot`	`\bigcirc`	`\dagger`	`\ddagger`
`\amalg`

pozn: pro \lhd, \rhd, \unlhd a \unrhd je potřeba standartní balík latexsym

Symboly ke kterým se obvykle přidávají indexy (které jsou často nad a pod):

`\sum`	`\prod`	`\coprod`	`\int`	`\oint`
`\bigcap`	`\bigcup`	`\bigsqcup`	`\bigvee`	`\bigwedge`
`\bigdot`	`\bigotimes`	`\bigoplus`	`\biguplus`

Příklad: $$\sum_{i=0}^\infty g_i$$ nebo $$\int_0^\infty f\,dx$$ V samostatném (vysázeném) vzorci se indexy k těmto symbolům umisťují nad a pod na rozdíl od vzorce v textu. TeXovský příkaz \limits (napsaný těsně za symbolem) však umožňuje i v textu vnutit psaní indexu nad a pod, např: $\int\limits _0^1$. Pokud chceme, aby indexy nebyly nad a pod i ve vysázeném vzorci, můžeme použít analogický příkaz \nolimits.

Další různé symboly:

`\aleph`	`\hbar`	`\imath`	`\jmath`	`\ell`
`\wp`	`\Re`	`\Im`	`\mho`	`\prime`
`\emptyset`	`\nabla`	`\surd`	`\top`	`\bot`
`\\|`	`\angle`	`\forall`	`\exists`	`\neg`
`\flat`	`\natural`	`\sharp`	`\backslash`	`\partial`
`\infty`	`\Box`	`\Diamond`	`\triangle`	`\clubsuit`
`\diamondsuit`	`\heartsuit`

pozn: pro \Box a \Diamond je potřeba standartní balík latexsym

Funkce:

`\arccos`	`\arcsin`	`\arctan`	`\arg`	`\cos`	`\cosh`	`\cot`
`\coth`	`\csc`	`\deg`	`\det`	`\dim`	`\exp`	`\gcd`
`\hom`	`\inf`	`\ker`	`\lg`	`\lim`	`\liminf`	`\limsup`
`\ln`	`\log`	`\max`	`\min`	`\Pr`	`\sec`	`\sin`
`\sinh`	`\sup`	`\tan`	`\tanh`

Řecká abeceda:

\Upsilon\upsilon

`\alpha`	`\betta`	`\Gamma`	`\gamma`	`\Delta`	`\delta`
`\epsilon`	`\varepsilon`	`\zeta`	`\eta`	`\Theta`	`\theta`
`\vartheta`	`\iota`	`\kappa`	`\Lambda`	`\lambda`	`\mu`
`\nu`	`\Xi`	`\xi`	`\o`	`\Pi`	`\pi`
`\varpi`	`\varrho`	`\Sigma`	`\sigma`	`\varsigma`	`\tau`
`\Phi`	`\phi`	`\varphi`	`\chi`
`\Psi`	`\psi`	`\Omega`	`\omega`

Závorky a příbuzné oddělovače: (je dobré je uvést příkazem \left nebo \right - pak se automaticky zvolí vhodná velikost)

( )	[ ]	`\{` `\}`	`\langle`	`\rangle`	`\lfloor`	`\rfloor`
`\lceil`	`\rceil`	`\uparrow`	`\downarrow`	`\updownarrow`	`\Uparrow`
`\Downarrow`	`\Updownarrow`	\|	`\\|`	/	`\backslash`

Pokud má na jedné straně závorka chybět, je třeba místo oddělovače použít tečku. Příklad:

    $$f(x) = \left\{ \begin{array}{r@{\quad}c}
              y, & x > \pi \\
             -y, & x \leq \pi \\ \end{array} \right.
    $$

Některé akcenty nad znakem v matematice:

`\hat{},`	`\tilde{},`	`\bar{},`	`\vec{},`	`\dot{},`	`\ddot{}` (dvě tečky),
`\acute{}` (čárka)

Spodní index - vytváří se za pomocí podtržítka (např. a_1 nebo a_\infty nebo a_{23}, když je index předepsán jako více znaků, pomůžeme si skupinou - např. a_{23}, funguje samozřejmě i např. toto a_\mathbf{23})

Horní index - naprostá analogie se spodním indexovánim, pouze místo podtržítka je nyní stříška (např. x^2).

Dají se samozřejmě vytvářet i indexy k indexům (např. x_{2_1}, ale musí se dát pozor na závorky - např. \int_0^1 je integrál od nuly do jedné;

Zlomky: vytváří se pomocí \frac{čitatel}{jmenovatel} (např. \frac{\sqrt{x}}{\pi}).

Některé další příkazy v matematickém režimu: \widehat{} \widetilde{} \imath a \jmath (i a j bez tečky) \stackrel{}{} (umístí první parametr v indexove velikosti nad druhý parametr Příklad: $U\stackrel{lim}{\rightarrow}V$)
\underbrace{} a \overbrace{} (vytvoření vodorovné svorky pod a nad objektem), ve vzorci mimo text lze \underbrace nebo \overbrace opatřit indexem - pak se tento index umístí pod nebo nad svorku (např. $$\underbrace{a_1+\overbrace{a_2+\cdots +a_9}^8+a_{10}}_{10}$$) \sqrt[]{} (např. $\sqrt[m]{1+x}$ nebo $\sqrt[{\textstyle m}]{1+x}$ )

\not - přeškrtnutí vpravo - znak za \not bude škrtnut; příklad: \not>; funguje tak, že se překrývá tento znak přeškrtnutí s následujícím znakem; polohu přeškrnutí vzhledem k objektu lze tedy ovlivnit vložením vhodné mezery mezi \not a znak; Pokud je znak symbol, vše funguje jak bylo řečeno, jinak může být potřeba uzavřít znak do složených závorek.

Různé tečky:: \ldots (lze použít i v textovém režimu), \cdots, \vdots, \ddots

Desetinné číslo v matematickém režimu - např. $1{,}345$ .

Mezery v matematickém režimu:: \! záporná uzká mezera, \; široká mezera, \ mezislovní mezera,
\, úzká mezera, \: střední mezera, \quad čtverčík, \qquad dva čtverčíky

Předchozí

Další

Nahoru

Obsah